DFT计算分析电荷转移方法有哪些？
密度泛函理论（Density Functional Theory,DFT）是一种广泛应用于材料科学、化学和物理学领域的量子化学计算方法。它通过计算系统的电子密度来描述分子或固体的电子结构，从而预测材料的物理和化学性质。在电荷转移研究中，DFT提供了多种工具和方法，用于分析和理解电荷在不同原子或分子之间的转移过程。本文将详细探讨DFT在电荷转移分析中的应用，包括差分电荷密度、Bader电荷、功函数、HOMO-LUMO能隙、静电势和态密度等方法。
差分电荷密度
差分电荷密度（Differential Charge Density,DCD）是DFT中用于分析电荷转移的一种重要方法。它通过比较两个系统之间的电荷密度差异，揭示电荷转移的方向和程度。 在Fe、Co等金属与基底之间的电荷转移中，由于d电子未填满，电荷在金属与基底间双向流动，体现强轨道耦合。而Cu、Zn因d轨道全充满，仅显示绿色耗散区，说明电子从金属单向转移到gC₃N₄，符合其弱还原性。碱金属（Na、Li、K）因电负性极低，绿色耗散区集中在原子周围，证实电子完全离域到基底，形成离子键特征。 非金属中，B在键合区积累电荷，显示共价键形成；O因高电负性吸引电子，导致自身周围强积累而键合区耗散，呈现极性键；S和P则因中等电负性同时存在积累与耗散，反映混合键合特性。整体上，差分图不仅验证了电负性差异驱动的电荷转移方向，还通过空间分布揭示了键合类型（离子/共价/极性），为理解掺杂原子与gC₃N₄的相互作用机制提供了直观电子尺度证据。Bader电荷
Bader电荷是基于Bader提出的“原子中的原子”（Atoms in Molecules,AIM）理论计算的一种电荷划分方法。该理论通过分析电子密度的拓扑结构（如临界点、梯度路径等），将分子或固体中的电荷密度分布划分为不同的原子区域（Bader体积），并通过积分每个区域内的电子密度来确定原子的净电荷。Bader电荷的计算公式为：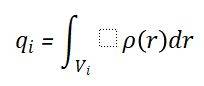
其中，qi表示第i个原子的净电荷，ρ(r)是空间r处的电子密度，Vi是第i个原子的Bader体积。Bader电荷的计算不仅能够确定电荷转移的净量，还能定位电子转移的空间分布，从而全面解析化学键的本质（共价、离子或金属键）。因此，Bader电荷是理论计算和材料模拟中不可或缺的工具，为理解电子结构调控和化学反应机制提供了坚实的理论基础。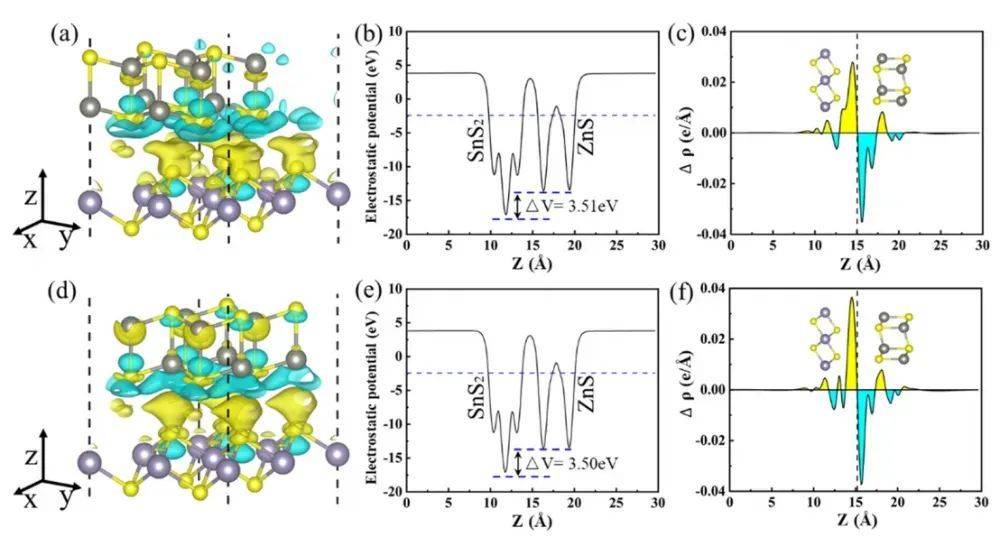
功函数
功函数（Work Function,φ）是指将一个电子从固体内部刚刚移到表面所需克服的最小能量，它等于真空能级与固体费米能级之间的能量差，数学表达式为：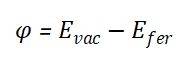
其中，φ表示功函数，Evac是真空能级，Efer是固体的费米能级。真空能级是电子在真空中具有的能量，而费米能级是固体中电子的化学势，反映了电子在固体中的填充水平。当两种不同材料相互接触或发生化学反应时，由于它们的功函数不同，会导致电子在界面处发生转移，以达到新的电子平衡状态。功函数较低的材料会失去电子，功函数较高的材料会获得电子，直到两者的费米能级对齐。通过测量或计算材料的功函数，并分析其在不同条件下（如吸附、掺杂等）的变化，可以推断出材料表面或界面处的电荷转移情况。HOMO-LUMO能隙
HOMO-LUMO能隙（HOMO-LUMO Gap）是描述分子得失电子难易程度的重要参数。HOMO（Highest Occupied Molecular Orbital）是分子中最高占据的分子轨道，LUMO（Lowest Unoccupied Molecular Orbital）是分子中最低未占据的分子轨道。HOMO-LUMO能隙的大小反映了分子得失电子的难易程度，能隙越小，分子越容易发生电荷转移。在有机光伏材料中，给体材料的HOMO能级与受体材料的LUMO能级之间的能量匹配对于电荷分离和转移至关重要。
HOMO能级的位置（如Macauromondo的-9.97eV）和LUMO能级（如-0.03eV）的相对能量差决定了电荷转移的方向性——电子通常从高能级的HOMO流向低能级的LUMO。
这种能级匹配关系在远程桥接的2,3,8-核体系中尤为明显，进一步证实了HOMO-LUMO分析在预测电荷转移路径中的重要性。通过HOMO-LUMO能级和能隙的分析，可以清晰地揭示分子内或分子间电荷转移的驱动力和方向性，为理解电子转移过程提供了关键的理论依据。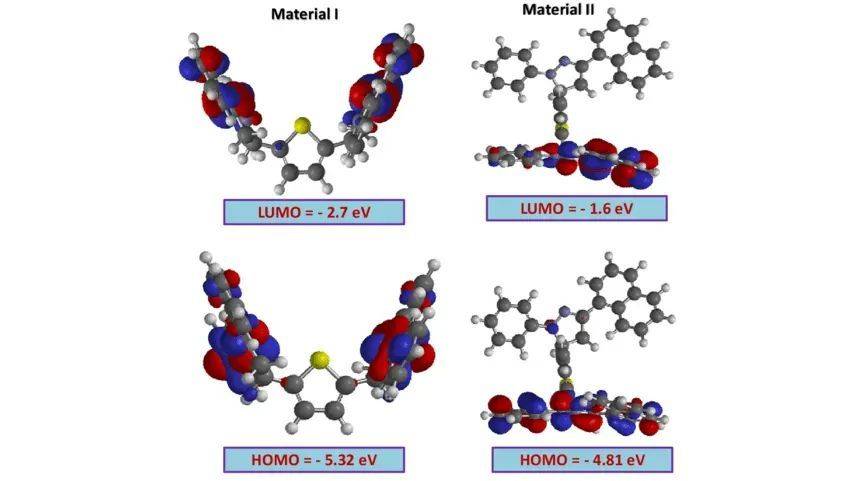
静电势
静电势（Electrostatic Potential,V(r)）是指在空间某一点处，将一个单位正电荷从无穷远处移动到该点时所做的功，它是描述体系电子结构的一个重要物理量。在DFT计算中，静电势可以通过求解泊松方程从电子密度计算得到，其数学表达式为：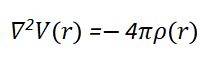
其中，V(r)表示空间r处的静电势，ρ(r)是空间r处的电子密度。静电势反映了体系中电子和原子核的电荷分布对空间电场的影响。当两个组分（如分子与基底）接近时，电荷倾向于从高静电势区（电子供体）流向低静电势区（电子受体）。因此，静电势能够分析电荷转移，关键在于其直观体现电子给/受能力。态密度
态密度（Density of States,DOS）是描述材料中电子能级分布的函数，表示单位能量区间内允许的电子量子态数量。态密度可分为总态密度（TDOS）和分波态密度（PDOS），后者进一步分解为原子轨道（s、p、d、f）的贡献，从而揭示不同轨道的电子结构特征。通过投影态密度（PDOS）分析揭示了HF分子在Li₂MnO₃（001）表面吸附时的电荷转移机制。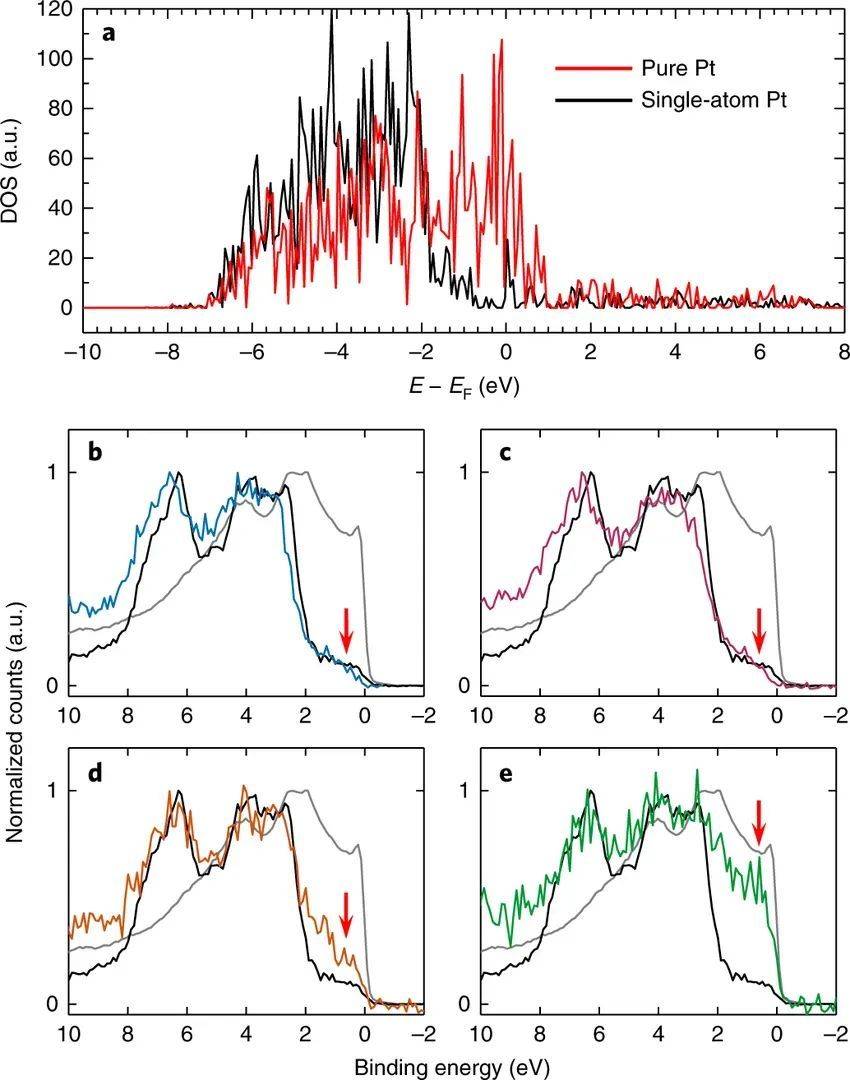
PDOS结果显示，Mn的d轨道在费米能级附近的贡献几乎未受HF吸附影响，表明Mn未直接参与电荷交换，与Bader电荷分析中Mn仅+0.02e的微小变化一致。关键变化集中在F和H的轨道上：F原子在-7.5eV附近出现新峰，对应其p轨道与表面Li的杂化，证实了F-Li的离子键相互作用；而H原子在-7eV附近的峰则指向H-O键的形成，解释了实验中H从HF解离后与表面O的键合。值得注意的是，随着HF覆盖度增加，F相关峰强度增强（0.06eV处），表明更高覆盖度下F的电子局域化更显著，可能增强表面钝化效应。
此外，费米能级附近未出现金属性新态，说明HF吸附未引入额外导电通道，而是通过F和H的轨道重构实现电荷再分配，降低了材料反应活性。态密度分析因此清晰地揭示了
电荷转移的原子尺度路径：电子从Li流向F形成极性键，同时H与O键合，而Mn保持惰性，这一机制为理解表界面修饰对材料电子结构的调控提供了重要依据。
总结
综上所述，差分电荷密度、Bader电荷等电荷布局、功函数、HOMO-LUMO、静电势和态密度这六种方法从不同角度为DFT计算中分析电荷转移提供了有力的工具。它们各自具有独特的定义和分析原理，在材料科学、化学、物理学等领域有着广泛的应用。通过综合运用这些方法，可以更全面、深入地理解电荷转移过程，为新材料的设计和性能优化提供坚实的理论基础。
在未来的研究中，随着DFT计算方法的不断发展和完善，这些分析方法也将不断拓展其应用范围和深度，为科学研究和技术创新提供更强大的支持。