一个本科生提出的全新物理量，如今能帮助科学家精确判断量子电路该用多深，避免资源浪费的同时提高计算效率。

量子计算机的核心——量子电路，正面临一个棘手难题：为了制备特定的量子态，电路太浅会导致制备不精确，太深又会浪费宝贵的量子资源。这个“深浅难题”一直困扰着量子计算科学家。

近日，首都师范大学物理系本科生祁硕以第一作者身份，在《物理评论快报》上发表重要成果，提出了一种全新的多体纠缠度量方法——χ-MPE。

这一方法能够帮助科学家判断变分量子电路的深度是否处于最优状态，为量子算法的设计和优化提供了可直接操作的理论工具。

01 量子电路的深度困境

量子电路作为量子计算机的核心部件，专门用于执行各类量子计算任务。与传统经典电路相比，量子电路面临诸多技术挑战。

在量子态制备环节，如何节省资源——包括减少量子门操作的数量、降低电路的复杂程度（即电路深度），成为亟待解决的关键科学问题。

这些因素不仅直接决定量子算法的运行效率与可扩展性，还与如何减轻噪声干扰、提高量子态稳定性密切相关，是推动量子计算走向实用化的重要前提。

科学家们一直面临一个核心两难困境：制备特定量子态时，电路太浅会导致量子态制备不精确，太深又会浪费资源。电路到底需要多深才算“刚刚好”？

02 本科生主导的突破性研究

近日，一项由首都师范大学物理系本科生祁硕作为第一作者的研究成果，在物理学顶刊《物理评论快报》上发表。

这项研究在冉仕举教授的指导下，与中国科学院理论物理研究所、莆田学院等多家单位合作完成，为量子电路深度优化难题提供了一个实用的解决方案。

研究团队将量子纠缠、张量网络与量子计算实现三者有机结合，提出了全新的多体纠缠度量方法，兼具重要的理论价值与广阔的应用前景。

这项工作的创新之处在于首次将张量网络流形与量子线路表达能力系统关联起来，为多体纠缠度量开辟了新路径，也为量子线路结构优化与算法设计提供了可操作的评估指标。

03 χ-MPE：量化多体纠缠的全新工具

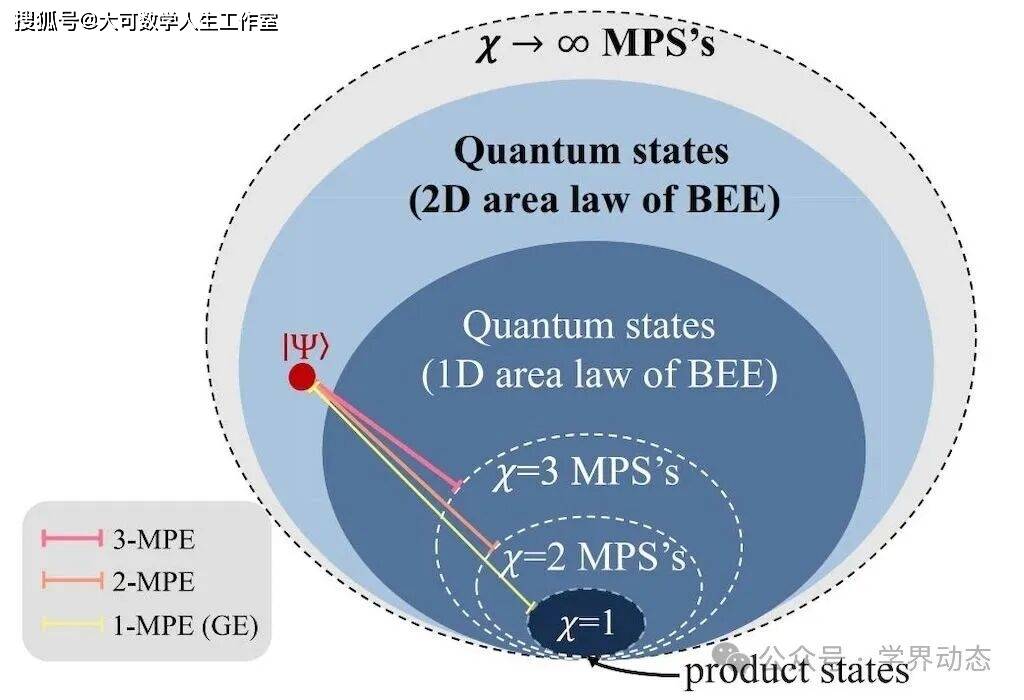
研究团队创新性地将矩阵乘积态作为参考流形，提出了全新的多体纠缠度量方法，引入了一个全新的物理量——特定χ矩阵乘积纠缠，简称为χ-MPE。

该方法的核心思想与传统几何纠缠不同，传统方法仅考虑与乘积态流形的距离，难以有效反映多体纠缠的复杂结构。

χ-MPE将目标量子状态与“最优”的张量网络状态进行比较。这里的“最优”是指目标状态与具有特定虚拟维度χ的MPS流形之间的最小保真距离。

当χ=1时，MPS退化成了最简单的“乘积态”，这时χ-MPE就变成了人们熟悉的“几何纠缠”，它衡量的是与完全没有纠缠的状态间的距离。

随着χ增大，流形覆盖的纠缠态范围逐步扩展，χ-MPE衡量的是与更复杂、但仍受限于特定复杂度纠缠态之间的距离。

04 三种标度关系破解电路深度之谜

研究团队进一步将χ-MPE与变分量子电路的“深度”联系起来。在量子计算中，电路的深度直接关系到计算的效率、对噪声的敏感度以及所需资源的多少。

研究发现，χ-MPE与量子电路制备目标状态的保真度之间存在奇妙的标度关系。他们通过理论推导和数值模拟，揭示了三种重要的标度行为。

超线性标度：当χ-MPE相对于态制备负对数保真度增长过快时，表明量子电路的深度是“过剩”的，电路太深了，浪费了量子资源。

线性标度：当χ-MPE与保真度近似成线性关系时，预示着量子电路的深度是“最优”的。论文给出了一个严格的证明：对于χ=2的MPS流形，它所代表的状态空间恰好等同于单层量子电路所能达到的状态空间。

亚线性标度：当χ-MPE相对于保真度增长得过慢时，说明量子电路的深度是“不足”的，电路太浅了。

05 量子计算优化的新路径

χ-MPE提供了一种新颖且可控的方式来量化多体纠缠，它与张量网络紧密结合，为理解复杂量子系统提供了新的工具。

通过分析χ-MPE与保真度的标度关系，可以直接判断当前变分量子电路的深度是否最优，从而指导量子算法的设计和优化，降低资源消耗，提高量子计算的效率和鲁棒性。

这种基于张量网络的方法可以推广到其他类型的张量网络结构，为评估更广泛的量子电路在制备各类张量网络状态时的最优性提供了可能。

这一成果展示了基础研究与实际应用之间的密切联系，本科生参与顶尖科学研究并取得突破性进展，也反映了中国量子计算领域人才培养的成果。

未来，这项研究框架可进一步推广到其他张量网络结构，用于评估各类量子态制备任务的线路效率。科学家们已经证明，对于χ=2的MPS流形，它所代表的状态空间恰好等同于单层量子电路所能达到的状态空间。

随着量子硬件的不断进步，这种精确指导电路设计的能力将变得越来越重要。量子计算机真正走向实用化的道路上，每一个量子门操作的优化都可能是突破瓶颈的关键。